
Les indices Skew Step sont des indices synthétiques générés algorithmiquement sur Deriv, qui combinent des tailles de pas inégales à des probabilités de mouvement asymétriques pour créer un comportement de prix structuré mais imprévisible. Conçus pour simuler certaines caractéristiques des marchés financiers réels sans être exposés aux actualités ou événements externes, ils offrent aux traders un environnement contrôlé dans lequel les mouvements dictés par les probabilités définissent à la fois les risques et les opportunités.
Contrairement aux indices Step classiques et Multi-Step, les indices Skew Step introduisent un biais directionnel ainsi que des retournements brusques occasionnels. Cela les rend adaptés aux traders recherchant plus qu’une simple action de prix uniforme, tout en profitant de mécanismes de marché transparents et basés sur des règles. Ce guide explique le fonctionnement des indices Skew Step, en quoi ils diffèrent des autres indices synthétiques, et comment les traders peuvent tirer parti de leur structure probabiliste pour élaborer des stratégies efficaces sur Deriv.
Résumé rapide
- Les indices Skew Step sont des indices synthétiques exclusifs à Deriv, définis par des tailles de pas inégales et des distributions de probabilité asymétriques.
- La plupart des mouvements de prix sont petits et fréquents, tandis que les mouvements plus importants sont plus rares mais ont un impact plus fort.
- Quatre indices sont disponibles : Skew Step 5 Up, Skew Step 5 Down, Skew Step 4 Up et Skew Step 4 Down.
- Leur conception fondée sur les probabilités permet d'appliquer des stratégies telles que le trading en range, la contre-attaque après pics et l'exploitation de la volatilité.
- Les indices Skew Step sont disponibles 24h/24 et 7j/7 sur Deriv MT5 et cTrader, avec la possibilité de trader en démo et de faire du backtesting.
Que sont les indices Skew Step ?
Les indices Skew Step sont un nouveau groupe d’indices Derived créés par Deriv pour offrir un mouvement de prix biaisé par la probabilité dans un cadre algorithmique transparent. Ils conservent la structure en pas des indices Step traditionnels tout en introduisant une asymétrie dans la direction et l’amplitude des variations de prix.
Caractéristiques clés des indices Skew Step :
- Tailles de pas variables : La majorité des ticks entraînent de petits changements de prix, tandis que les bonds importants sont plus rares.
- Probabilité asymétrique : Un mouvement directionnel est statistiquement plus probable qu’un autre, créant un biais directionnel intégré.
Génération algorithmique : Tous les mouvements de prix sont produits par des algorithmes de génération de nombres aléatoires utilisant des distributions de probabilité prédéfinies, indépendamment des données économiques ou des actualités de marché.
Cette conception permet aux traders d’anticiper un comportement typique tout en restant exposés à des pics imprévus à fort impact.
Indices Skew Step vs indices Step et Multi-Step
Comparaison des structures d’indices synthétiques
| Caractéristique | Indices Step | Indices Multi Step | Indices Skew Step |
|---|---|---|---|
| Tailles de palier | Unique, fixe | Multiples, symétriques | Multiples, asymétriques |
| Probabilité directionnelle | Pair | Pair | Asymétrique |
| Comportement des prix | Uniforme | Mixte mais équilibré | Biais directionnel avec pics |
| Volatilité typique | Bas | Modérée | Modérée à élevée |
| Idéal pour | Trading systématique | Stratégies basées sur les modèles | Stratégies de volatilité et de retournement |
Les indices Classic Step privilégient la prévisibilité, tandis que les indices Multi Step introduisent de la variation sans biais. Les indices Skew Step se distinguent par une asymétrie probabiliste qui influence directement le comportement de la volatilité et le choix des stratégies.
Le fonctionnement des indices Skew Step
Chaque tick dans un indice Skew Step est généré à partir de deux décisions basées sur la probabilité :
- Sélection de la taille de palier : L'algorithme choisit une variation de prix dans un ensemble prédéfini.
Résultat directionnel : Le mouvement est orienté selon une distribution de probabilité asymétrique.
Les traders observent ainsi :
- De longues séquences de petits mouvements prévisibles dans une même direction
- Des mouvements importants occasionnels dans la direction opposée
- Une volatilité globale influencée par la fréquence et l’amplitude des mouvements
Exemple : Skew Step 5 Up
- Environ 90 % des ticks génèrent de petits mouvements à la hausse
- Environ 10 % entraînent des baisses marquées
Cette structure explique pourquoi des conditions de marché calmes peuvent être perturbées par des retournements soudains, créant à la fois des risques et des opportunités.
Gamme d’indices Skew Step et distributions de probabilité
Deriv propose actuellement quatre indices Skew Step, chacun présentant des caractéristiques de volatilité uniques.
Skew Step Index 5 Up
- 90 % de chances de petits mouvements à la hausse
- 10 % de chances de chute brutale
- Volatilité : 19,36 %
| Taille du pas | -1 | 0.1 | 0.2 | 0.3 | 0.4 |
|---|---|---|---|---|---|
| Probabilité | 10% | 83 % | 5% | 1 % | 1 % |
Skew Step Index 5 Down
- 90 % de chances de petits mouvements à la baisse
- 10 % de chances de Rise brutale
- Volatilité : 19,36 %
| Taille du pas | 1 | -0.1 | -0.2 | -0.3 | -0.4 |
|---|---|---|---|---|---|
| Probabilité | 10% | 83 % | 5% | 1 % | 1 % |
Skew Step Index 4 Up
- 80 % de chances de petits mouvements à la hausse
- 20 % de chances de chute brutale
- Volatilité : 14,30 %
| Taille du pas | 1 | -0.1 | -0.2 | -0.3 | -0.4 |
|---|---|---|---|---|---|
| Probabilité | 10% | 83 % | 5% | 1 % | 1 % |
Skew Step Index 4 Down
- 0 % de chances de petits mouvements à la baisse
- 20 % de chances de Rise brutale
- Volatilité : 14,30 %
| Taille du pas | 0.5 | -0.1 | -0.2 | -0.3 |
|---|---|---|---|---|
| Probabilité | 20 % | 65 % | 10% | 5% |
En quoi diffèrent-ils des indices step et multi-step ?
Les Step Indices ont des tailles de pas fixes et des probabilités symétriques. Les Multi-Step Indices mélangent les tailles de pas mais gardent des probabilités égales. Indices Skew Step? Ils font les deux : différentes tailles de pas et probabilités inégales. Cela signifie que les mouvements de prix sont plus imprévisibles, apportant un tout nouveau niveau d'excitation et d'opportunités au trading synthétique.
| Indice | Description | Taille du pas | Probabilité |
|---|---|---|---|
| Step 200 | Taille de pas fixe avec chance égale de monter ou descendre | ±0.2 | 50% |
| Multi Step 2 | Tailles de pas multiples avec chance symétrique de monter ou descendre | ±0,5 | 2,5% |
| ±0.1 | 47,5 % | ||
| Skew Step 4 Up | Tailles de pas multiples avec chance asymétrique de monter ou descendre | -0.5 | 20 % |
| +0.1 | 10% | ||
| +0.3 | 5% |
Comprendre la volatilité est essentiel ici. Les Skew Step Indices proposent un compromis entre les Step et Multi-Step Indices. Le graphique comparatif de volatilité ci-dessous montre comment ils se positionnent.
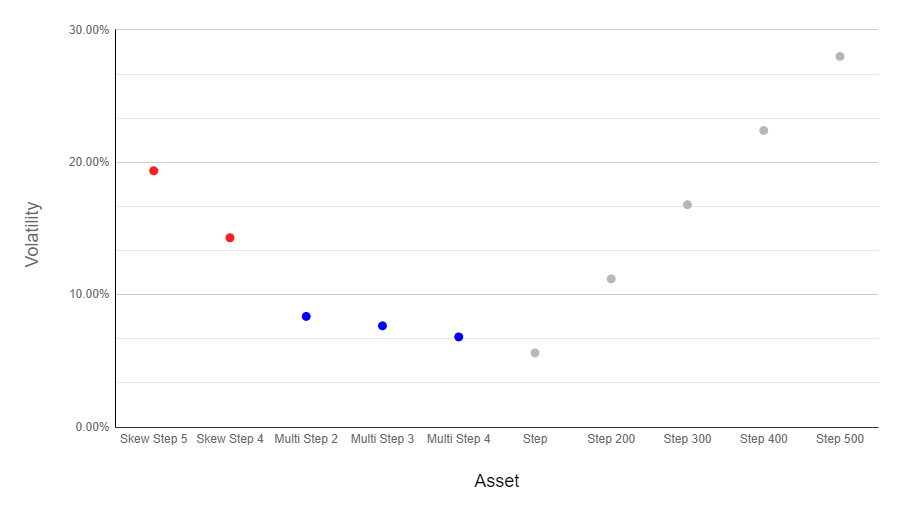
Comportement de la volatilité et expérience de trading
La volatilité des indices Skew Step n’est pas constante. Elle résulte du contraste entre de nombreux petits mouvements et des mouvements importants rares, plutôt que de grandes fluctuations continues du prix.
| Type d'indice | Comportement typique | Profil de volatilité |
|---|---|---|
| Step | Mouvement uniforme | Bas |
| Multi Step | Mixte mais équilibré | Modérée |
| Skew Step | Majoritairement petits, parfois importants | Modérée à élevée |
Étant donné que les mouvements importants sont rares mais décisifs, la volatilité a tendance à se concentrer autour d’événements exceptionnels plutôt qu’à se répartir uniformément dans le temps.
Pourquoi trader les indices Skew Step ?
Les indices Skew Step attirent les traders qui recherchent des marchés informés par la probabilité avec un comportement dynamique :
- Application stratégique élargie : L’asymétrie probabiliste favorise le range trading en conditions normales et les stratégies de retournement après des mouvements rares.
- Comportement réaliste des prix : Les sauts soudains introduisent une incertitude propre aux marchés réels sans facteurs de risque externes.
- Transparence totale : Les distributions de probabilité publiées permettent aux traders de planifier précisément leurs paramètres de risque.
- Accès ininterrompu : Le trading est disponible 24h/24, 7j/7, week-ends et jours fériés inclus, exclusivement sur Deriv.
Comment trader les indices Skew Step sur Deriv
- Ouvrez un compte Deriv
- Inscrivez-vous pour un compte réel ou entraînez-vous sans risque avec un compte démo.
- Inscrivez-vous pour un compte réel ou entraînez-vous sans risque avec un compte démo.
- Choisissez une plateforme de trading
- Tradez sur Deriv MT5 pour des analyses techniques avancées et stratégies automatisées, ou utilisez cTrader pour une interface épurée.
- Tradez sur Deriv MT5 pour des analyses techniques avancées et stratégies automatisées, ou utilisez cTrader pour une interface épurée.
- Trouvez les indices Skew Step
- Recherchez « Skew Step » dans la surveillance de marché pour voir toutes les variantes disponibles.
- Recherchez « Skew Step » dans la surveillance de marché pour voir toutes les variantes disponibles.
- Analysez le graphique
- Appliquez des indicateurs tels que RSI, moyennes mobiles ou bandes de Bollinger pour repérer les changements de momentum et de volatilité.
- Appliquez des indicateurs tels que RSI, moyennes mobiles ou bandes de Bollinger pour repérer les changements de momentum et de volatilité.
- Testez et exécutez des stratégies
- Utilisez des données historiques et le trading démo pour évaluer les performances avant de trader en réel.
- Utilisez des données historiques et le trading démo pour évaluer les performances avant de trader en réel.
Considérations stratégiques pour les indices Skew Step
- Range trading : Efficace lors de longues séquences de petits mouvements fréquents.
- Atténuation de pic : Les mouvements importants rares entraînent souvent des corrections à court terme en raison du retour à la moyenne probabilistique.
- Poursuite du momentum : Certains traders choisissent de suivre le mouvement rare lorsqu’il rompt une structure de prix établie.
- Gestion du risque : Des tailles de position plus petites et des niveaux de stop-loss plus larges permettent de mieux gérer l’exposition à la volatilité soudaine. Découvrez-en plus sur la gestion du risque et la taille des positions dans notre guide sur la taille des positions.
Les indices Skew Step offrent une approche structurée mais flexible pour trader les marchés synthétiques. En combinant des probabilités définies à une volatilité variable, ils permettent aux traders d’explorer des stratégies disciplinées dans un environnement transparent et toujours accessible sur Deriv.
Commencez à trader les indices Skew Step avec un compte démo gratuit et développez votre stratégie de trading autour de ces indices sans risquer vos fonds.
Quiz
Laquelle des affirmations suivantes décrit le mieux les indices Skew Step ?
















